

蓝牙到达角(AoA)和出发角(AoD)技术给室内定位标准带来新框架。利用此技术,室内定位的基本问题可分为判断射频信号的到达角和离开角。现在有很多企业开始在AoA/AoD上投入研发力量。

定位功能是户外应用需求中备受关注的功能,定位技术中不乏有很多实用的应用,例如在世界各地被广泛运用的GPS。
在室内环境无法使用GPS等卫星定位时,需要更精确的室内定位技术。使用室内定位技术作为卫星定位的辅助定位,可以有效解决卫星信号到达地面时穿越建筑困难的问题,最终定位物体当前所处的位置。
蓝牙5.0标准发布以来,越来越多基于蓝牙5.0的应用被开发出来。现在,室内定位技术AoA/AoD建立室内定位新框架,利用蓝牙寻向算法,使室内定位更加精准简单。

蓝牙AoA/AoD技术使用外部追踪系统测量某个对象的位置或角度,追踪设备在室内环境中的位置。这种定位系统可以运用于仓库的物流追踪或商场顾客位置追踪,人们可以将其用于定位寻路。
AoA技术以接收器和发射器为基础。例如,一个多天线线性数组的设备作为接收器,另一个单天线的设备作为发射器,假设无线电波作为平面波面而非球形。如果在空中发送正弦波的发射器,位于与数组线垂直的法线,则数组中的每个天线将接收相同相位的输入讯号。如果发射器不在法线,则接收天线将测量信道之间的相位差,利用相位差信息估算到达角度。
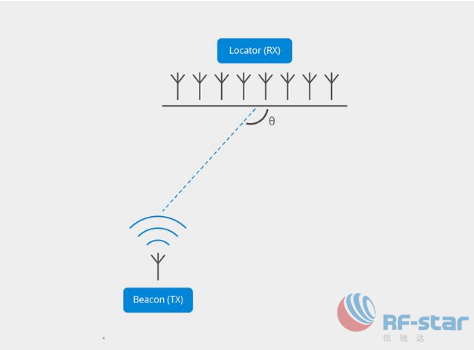
无线电波以300,000km/s的光速传播。采用大约2.4GHz频率时,相应波长约0.125m。大多数估计算法中,两个相邻天线之间的最大距离是半波长。许多算法都须满足这项条件,否则将导致失真。理论上并没有最短距离限制,但实际上,最小尺寸受限于数组的机械尺寸,譬如天线各组件之间的相互耦合。
对于出发角,测量相位差的基本原理是相同的,但装置角色互换。在AoD中,被追踪的装置仅使用一个单天线,而发射器装置则使用多天线。发射装置依序转换发射天线,让接收侧了解到天线数组架构并转换序列。从应用的角度,能发现这两种技术之间存在明显差异。在AoD中,接收装置根据多个目标角度和位置计算本身在空间中的位置。在AoA中,接收装置追踪各个对象的到达角度。

在蓝牙AoA与AoD中,相关的控制数据通过传统的数据信道传输。通常这些技术能测量出精确的角度和0.5公尺左右的定位精度,且高度依赖定位系统产生的数据。
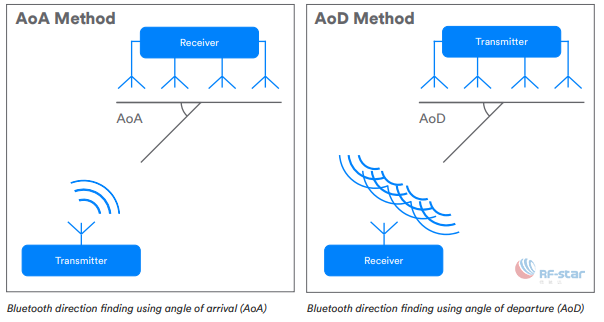
此外,讯号噪声、频率抖动和信号传输延迟,也会对角度估算法造成很多影响。根据系统规模,如果在嵌入式系统中,对于RAM尤其是CPU的要求可能非常严格,许多高效能的角度估算法需要具备强大处理能力的CPU才能执行。
现在的室内定位技术中,很多运用的是RSSI进行定位。接收讯号强度指示(RSSI)测量接收讯号的讯号强度来获得RX和TX之间的近似距离。该信息可运用于来自不同发射器位置的多点距离测量,三角定位接收器的位置。此技术中,每个装置只需要一个天线,在室内环境却通常不够准确。
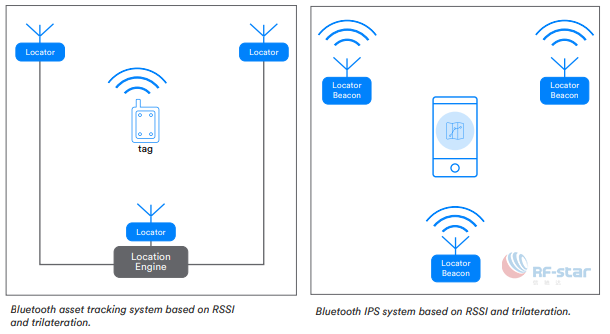
利用到达时间/飞行时间(ToA/ToF),可测量RX和TX之间的讯号传输时间,并计算两端点的距离。再用此距离三角定位接收器的位置。
AoA/AoD是新兴技术,可用于资产追踪以及室内定位和寻路。这些相位基础的寻向系统,需要天线数组、RF开关来运行估计算法。设计适合的天线数组和角度估计算法,对RTLS系统至关重要。而效能强大的估计算法在运算上通常不便宜。其他定位技术包括RSSI基础方法和ToA基础方法,但目前,只有相位基础的AoA/AoD在蓝牙中具有标准架构。
蓝牙室内定位功能在市面上已有很多成熟的案例,例如在零售领域,将传统的灯具切换成具备蓝牙Beacon能力的智能灯后,可以帮助客户和员工在商场里导航,并更快、更容易地找到商品。商家也可以利用蓝牙信标进行个性化促销,以创造更好的购物者体验,增加销售额。
蓝牙室内定位功能也能给用户带来更有趣味的体验,在博物馆里,具备蓝牙功能的LED模组和传感器可以检测温度和湿度水平,以帮助保护无价的艺术品,同时减少维护和日常开销。这些智能设备可以提供兴趣点信息和寻路服务,以增强游客体验。
各科技公司在AoA/AoD技术应用的投入,势必将会为室内定位应用方案带来更多更合适的选择。
附:AoA/AoD估计算法原理
透过寻向剖析AoA/AoD理论
角度估算方法和天线数组对定位系统的正常运作至关重要。定位寻向(Direction Finding)理论的历史可追溯至一百多年前,试图采用定向天线解决这个问题,而当时显然是单纯的模拟系统。接下来的数年中,测试方法转移到数字世界,但基本原理仍然非常类似。这些寻向方法已被广泛的应用,例如医疗器材、安全和军事设备。
在本段落中,将讨论一些典型天线数组和估计算法的基础概念。藉由寻向,进而涉及估算到达角和出发角的基本问题。
天线数组
用于寻向的天线数组可分为几种类型。这里讨论的是最普遍的均匀线性数组(ULA)、均匀矩形数组(URA)和均匀圆形数组(UCA)。线性数组是一维数组,这是指数组中所有天线皆位于一条在线,而矩形和圆形数组则是二维数组,意味天线分布于两个维度(在一个平面上)。透过一维天线数组,假设被追踪的装置始终在同一平面上移动,便能可靠测量出方位角。但透过二维数组,能进一步测量出3D半空间中的方位角和仰角。假若数组扩展成完整的3D数组(天线分布于三个直角坐标上),便能测量完整的3D空间。
设计用于寻向的天线数组不是一项简单的任务。天线置于数组中时会彼此影响,这称为互相耦合。多数情况下,设计者无法控制发射端的极化。这为设计人员带来额外的挑战。在物联网(IoT)应用中,通常默认这些装置很小,甚至在高频段中运作。估计算法通常具备某些数组特性,例如ESPRIT估计算法,数学假设上数组被分为两组相同的子数组。
角度估计算法
接下来,看看输入IQ数据来估算到达角的数学/算法问题。问题定义很简单:估算发射(窄频)讯号抵达接收数组的到达角。虽然这项陈述看似微不足道,但是对这个问题而言,寻找到一个强效(且在现实中运行)的解决方案并不容易,强大的硬件处理能力也相当关键。
接下来,将介绍两种不同解决方法。第一种是基本的,经典波束成形器。第二种是较先进的技术,多重讯号分类(MUSIC)。在此不会用任何定理或原因验证这些方法的工作原理,仅用高视野来探讨算法如何运作。
经典波束成形器
从均匀线性数组的数学模型谈起。假设每个天线对应一个IQ样本的数据向量称为x。在测量中,每个天线都可以看到相移(可能为0)加上一些噪声n,所以x可以计算时间函数t:

其中,s代表空中的发射讯号,a是天线数组的导引向量。
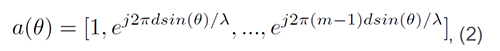
d是相邻天线之间的距离;λ是讯号波长;m是天线数组中的组件数量,θ代表到达角。
导引向量(2)描述各个天线上的讯号,因为到达发射器的距离变化而相移。藉由(1),可以计算出所谓的样本共变异数矩阵Rxx近似值:
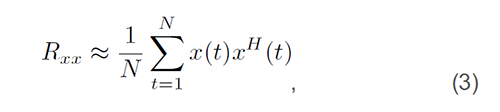
H代表Hermitian转置矩阵。
可看到样本共变异数矩阵(3)将作为估计算法的输入数据。
经典波束成形器的概念是最大化输出功率作为角度的函数,类似机械雷达的运作方式。若要将功率最大化,最终可得出以下公式:

为了找出到达角,须要代入到达角θ并计算功率P的最大值。产生最大功率的角度或θ对应的到达角。
多重讯号分类(MUSIC)
这种估计算法是所谓的子空间估算,其中盛行的一种算法称为MUSIC(多重讯号分类)。这个算法的概念是对共变异数矩阵Rxx进行特征分解:
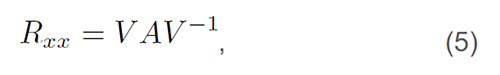
其中,A是包含特征值的对角矩阵,V是包含Rxx的对应特征向量。
假设,尝试计算一个发射器采用n天线线性数组的到达角。可以证明,Rxx的特征向量或者属于所谓的噪声子空间或属于讯号子空间。如果特征值按升幂排序,对应的n-1特征向量跨越噪声子空间,该子空间与讯号子空间正交。从正交信息,可以计算伪频谱P:
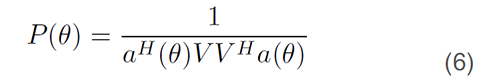
在经典波束成形器中,不断代入期望θ值来计算P的最大值,其对应于我们期望测量的到达角(参数θ)。
理想情况下,MUSIC在良好的SNR环境中具有出色的分辨率,而且非常准确。另一方面,当输入讯号高度相关时,特别在室内环境中,效能较弱。多径效应使伪频谱失真,导致在错误的位置产生最大值。
空间平滑化
空间平滑化是解决由多径(产生相干讯号时)所引发问题的一种方法。可以证明,利用原始共变异数矩阵的子数组可以计算出平均共变异数矩阵,让讯号共变异数矩阵「去相干」。对于二维数组,公式可写成:
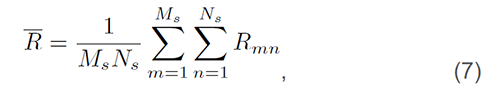
其中,MS和NS分别是x和y轴上的子数组数,Rmn代表(m,n):子数组共变异数矩阵。
由公式得到的共变异数矩阵便是共变异数矩阵的「去相干」版本,输入到MUSIC算法便能产生正确结果。空间平滑化的缺点是它缩减了共变异数矩阵的大小,降低估算的准确性。